이안 말콤 박사 - 제프리 린 골드블럼(Jeffrey Lynn Goldblum)
다른 고생물학자들과 달리 이안 말콤 박사는 수학자로 주로 “혼돈 이론” 즉 카오 이론 “Chaos Theory”을 연구하였다. 생물학자가 아닌 수학자 이안 말콤의 명언 “음 생명은 항상 길을 찾는다” “Life, uh, finds its way”은 쥬라기 공원과 쥬라기 월드를 모두 관통하는 주제가 된다.
이안 말콤 박사는 조프리 브라운 노동자의 벨로시 랩터 우리 사망사건의 일환으로 마련된 쥬라기 공원 개방에 대한 결정을 위한 조사단으로서 쥬라기 공원 개장에 초대 받는다.




이안 말콤 박사는 처음부터 쥬라기 공원 자체를 하나의 혼돈계로 해석하고 ‘생명'이라는 너무나 다양한 변수를 가진 주체를 통제할 수 있을거란 인젠의 망상에 부정적이었다.
이안 말콤의 생각과 쥬라기 공원 전체 주지를 대변하는 생명은 길을 찾는다는 말로 이를 함축적으로 표현된다. 이안 말콤 박사는 티라노사우루스 렉스의 습격을 받은 후 구출 되고 모두와 함께 코스타 리카의 병원에서 치료 받는다. 이때 이안 말콤 박사의 여자친구 사라 하딩이 그를 찾는다.




이안 말콤 박사는 인젠사와 쥬라기 공원에 대한 비밀 유지 협약을 맺었지만 이안 말콤 박사는 계속해서 공룡에 대한 그릇된 야망을 품는 인젠 회사에 대항하텨 이슬라 누블라 섬의 쥬라기 공원 사태에 대한 회고록을 출판한다.
인젠사는 언론에 막대한 보상금을 지불하고 여론을 조작하여 이안 말콤 박사를 미친 사람이나 바보로 만들어버렸다. 제프리 린 골드블럼 또는 제프 골드블럼은 이안 말콤 받사를 연기하였으며, 제프 골드블럼은 위성 동학자 데이비드 레빈슨 역으로 인디펜던스 데이에 출연을 하고 마블 시네마틱 시리즈의 토르 라그나로크에서 그랜드 마스터 역을 연기하기도 하였다.




엘리 새틀러 박사의 손에 물을 떨어뜨리는 이안 말콤 박사의 실험 설명 - 혼돈 이론
이안 말콤 박사는 플러팅도 할겸 엘리 새틀러 박사에게 혼돈 이론을 설명 해주겠다면서 손을 달라고 한다. 하지만 이 마냥 바람둥이 같은 이안 말콤 박사의 물방울을 손에 떨어뜨리는 실험을 통해 혼돈 이론이 간단하지만 설명이 된다.
이안 말콤 박사는 물방울 하나를 엘리 새틀러 박사의 손에 떨어뜨리고 다음 물방울이 떨어지는 방향을 예측해달라고 한다.
이안 말콤 박사가 물을 떨어뜨리는 높이, 위치나 모든 변수들이 동일하다고 생각한 엘리 새틀러 박사는 당연히 첫 물방울이 떨어진 방향대로 물방울이 떨어질거라고 말한다. 이안 말콤 박사는 정확히 똑같은 위치, 높이 속도 등을 모두 동일하게 엘리 새틀러 박사의 손에 물방울을 떨어뜨리지만 물방울은 완전히 다른 방향으로 떨어진다.



이안 말콤 박사는 모든 변수들이 처음과 같이 똑같다고 생각함에도 불구하고, 첫 물방울을 떨어뜨린 순간 엘리 새틀러 박사의 피부에 닿은 순간 혈관의 이완과 수축, 기공의 크기, 체온의 상승과 하강 등 변수들로 인해서 사실은 모든 것이 처음과 동일한 조건이 아니기 때문에 물방울의 방향은 예측이 불가한 방향으로 갔다고 설명한다. 이안 말콤 박사는 이처럼 초기 변수의 값에 민감하게 반응하는 것이 간단하게 혼돈이론이라고 설명해준다.
이안 말콤 박사는 혼돈이론에 의거하면 엘리 새틀러 박사의 손에 떨어뜨리는 물방울이 흐를 방향 조차도 예상이 안 된다는 사실을 간단한 실험과 여러 사실을 통해 알리면서 인간이 모든 변수들을 처음부터 고려하고 의사결정도 못할 뿐 더러 이 한 가지 변수라고 놓치면 생길 거대한 후폭풍은 예상 불가 하다는 복선을 남기며 왜 생명을 통제하고 신놀음을 하는 것이 위험한지에 대한 주제의식도 환기시킨다.




수학자인 이안 말콤 박사가 쥬라기 공원의 주제의 핵심인 이유
이안 말콤 박사는 엘리 새틀러 박사와 앨런 그랜트 박사와 같은 고식물 고생물 학자들과 달리 혼돈이론을 연구하는 수학자이다. 전혀 생명 윤리나 생물학과는 관련 없지만 이안 말콤 박사는 쥬라기 공원의 전체 주제를 함축하는 “생명은 음, 길을 찾는다” “Life, uh, finds its ways”를 통해 쥬라기 공원과 쥬라기 월드의 기본 사상이자 핵심 주제의 주인공이 된다.
유독 시리즈에서 이안 말콤 박사가 많이 출연하는 이유기도 하다. 공룡들의 창조에 대한 가상 토론 주제로서 실존 과학과 과학적 윤리의 대립, 신의 영역인 생명 창조에 대항하는 신학적인 대립 등의 주제도 일부 다루지만 쥬라기 공원은 그보다는 “통제 할 수 없는 자연" “자연 앞에 무력한 인간" “자연은 인간의 이해 영역 밖에 존재한다.”이라는 주제에 집중한다.



결국 쥬라기 공원이나 쥬라기 월드에 발생한 모든 사건들은 혼돈 이론에 따르면 모든 초기 변수들을 알 수 없어 전혀 예측이 불가함에도 그런 불확실성 속에서도 자연을 통제할 자연이 예측 범위 내에 존재한단 오만함에서 모두 비롯 된다.
결국 이안 말콤 박사가 혼돈 이론 즉 카오스 이론을 통해 설명하고자 한 것은 모든 초기 변수들도 계산 불가능 한 상태에서 미래는 예측은 불가하고 손에 물방울이 떨어지는 작은 반복적인 상황도 통제가 불가능한데 더군다나 변수가 많은 생명을 창조하고 통제할 수 있을거란 인젠 회사의 오만함을 비판하는 겻이였다.



따라서 이안 말콤의 대사 “Life finds its way” “생명은 길을 찾을 것이다.”는 공룡들을 절대 통제 할 수 없는 운명임을 시사하는 복선인 동시에 쥬라기 공원과 쥬라기 월드 안의 모든 인물들 또한 자신이 예측 못할 상황에서도 이를 헤쳐나가며 살아가는 것 또한 암시하는 복선이자 전체 쥬라기 공원 시리즈의 주제인 셈이다. 따라서 이안 말콤의 혼돈이론은 쥬라기 공원과 쥬라기 월드 시리즈의 모두를 관통하는 주제 의식이 된 셈이다.




혼돈 이론 - 카오스 이론 The Chaos Theory
혼돈 이론은 “비선형 역학계" “Non-Linear Dynamics”라고도 불리는 수학적인 개념에 대한 이론이다. 비선형 계란 어떤 변수를 입력하였을 때의 함수의 결과 값이 반드시 비례하지는 않음을 의미한다. 혼돈 이론은 흔히 나비 효과 “Butterfly Effect” 라는 설명으로 유명한데 이 나비 효과는 나비의 작은 날개짓이 폭풍 허리케인을 일으킬 수 있다는 생각이다.
이는 혼돈 이론을 완전히 대변하는 개념은 아니지만 아주 작은 변수의 차이에도 함수 값이 완전히 달라지는 혼돈 이론의 개념은 가진 효과이다. 혼돈 이론은 작은 변수에 의해 큰 결과가 나타남을 설명하기 보다는 이러한 변수와 결과 값 사이의 함수나 관계를 통해 나타난 시스템 (계)에 대해 탐구하는 수학 이론이다.

또한 혼돈 이론에서 설명하는 혼돈계 내에서는 관련성이 없는 무작위 랜덤 패턴이 사실은 어떤 변수의 입력과 결과값의 함수 관계 또는 인과관계가 있는지에 대해서도 공부하는 이론이다.
이 세상을 혼돈 이론에서 설명하는 혼돈계 즉 비선형 동역학계라고 가정을 하면 어떤 일에 대해서든 모든 변수들에 대해서 알지도 못하고 이들의 값이나 관련성 또한 모두 한번에 설명을 못하기에 결과적으로 이 세상이 향후 어떻게 될지 예측이 불가하다고 할 수 있다. 혼돈 이론에서는 미래를 예측 불가하다고 설명하는 이론은 아니다.

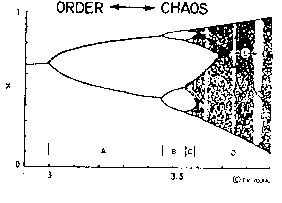
다만 혼돈계 안에서 미래를 예측 하기 위해서는 모든 변수들의 초기값과 결과와의 관계식이 있어야만 미래 예측이 가능하다고 설명한다. 쥬라기 공원 내에서 이안 말콤 박사는 단순히 미래는 예측이 불가하다고 반대를 하는 것이 아니라 이런 수학적인 논리에서 특히나 변수를 전혀 알 수 없는 신의 영역인 생명 창조에서 인젠이 그 어떤 결과도 간과해서는 안되고 사실상 이 영역에서는 미래도 예측이 불가하고도 주장하는 것이다.
이안 말톰은 “신은 공룡을 창조하고 신은 공룡을 멸망시키고, 신은 인간을 창조하고, 인간은 신을 살해하고, 인간은 공룡을 되살린다. 그럼?” 이란 대사를 통해 이를 나타낸다.
“God creates dinosaurs, God kills dinosaurs, God creates man, man kills God, man brings back dinosaurs.”
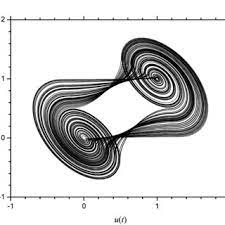



혼돈 이론에서 정의하는 혼돈계의 조건
1.시스템(계)는 초기 변수에 민감해야 한다.
2. 시스템(계)는 위상 혼합성 경향을 띠어야 한다. (Topological mixing)
위상 혼합성(토폴라지컬 믹싱 /Topological Mixing)을 띠는 시스템은 시스템 내에서 위상들이 혼합 될 수 있는 성질을 말한다. 쉽게 말하면, 시스템 내에서 어떠한 무작위의 집합들을 선택하더라도, 값의 이터레이션, 즉 선택한 집합들의 값이 시스템(계)내에 존재 할 때 (값의 반복, value iteration / 프로그래밍에서의 가치 반복과는 다름)의 경향을 위상 혼합성(Topological mixing)이라고 부른다.
3. 시스템(계)는 조밀한 주기적 궤도(dense periodic orbit)를 갖춰야 한다.
궤도(orbit)는 시간을 매개로 초기의 입력 값이 시간이 변함에 따라 나온 결과들의 집합을 의미한다. 주기적인 궤도(periodic orbit)란 특정 시간이 지났을 때, 궤도가 초기의 값으로 회귀하는 것을 뜻한다. 조밀한 주기적 궤도(Dense periodic orbit)는 주기적인 궤도들의 합집합이 조밀한 합집함을 이루면서 초기의 값에 모두 대응 할 때의 주기적인 궤도를 뜻한다.
혼돈 이론의 쉬운 예시 – 핀볼
수학적인 이론에서의 혼돈 이론은 매우 어려워 보이지만, 핀볼을 예시로 들면 쉽게 설명이 가능하다. 핀볼이 이루어지는 네모나 공간은 “조밀한 주기적인 궤도” (dense periodic orbit)라고 할 수 있다. 결국 핀볼이 위치 할 수 있는 모든 위치들의 합집합은 이 핀볼이 이루어지는 네모난 공간에 한정되어 있고, 시간이 지남에도 핀볼은 처음의 위치로 되돌아 온다.
또한, 이 네모난 상자 안은 아무리 많은 시간이 지나더라도, 어떠한 방식으로든 핀볼을 치더라도 한번은 핀볼이 지나칠 수 있는 확률을 가지고 있기 때문에 핀볼이 이루어지는 공간은 위상혼합성을 띤다고 할 수 있다.


핀볼을 아무리 똑 같은 힘이나 속도로 친다고 하더라도, 핀 볼은 아주 작은 변수에도 예민하게 반응하기에, 항상 다른 위치로 핀볼이 튄다. 즉, 이 핀볼 안의 계(시스템)은 초기 변수에도 예민하다고 할 수 있다.
혼돈 이론적인 관점에서도 핀볼은 혼돈계라고 할 수도 있고, 간단한 핀볼을 치는 것 조차도 항상 다른 결과를 가질 수 있다는 점에서 완전히 일치하지는 않지만 핀볼은 혼돈 이론을 설명하는 하나의 예시가 될 수 있다.
혼돈 이론의 초기 관념들 – 앙리 푸앵카레(Henri Poincaré)
앙리 푸앵카레는 프랑스의 수학자이자 이론 물리학자로, 많은 업적을 이루었다. 앙리 푸앵 카레는 태양계의 역사를 알고이 역사 동안 이루어진 수학적인 해석을 해야만 태양계의 미래를 예측하기 할 수 있다고 주장하였다.
이 시기 과학자들은 태양계의 처음 상태가 어떤지 알면 태양계의 미래 또한 예측할 수 있다고 주장을 하였는데, 앙리 푸앵카레는 “초기 변수의 민감성”이라는 개념을 제시하면서, 이들의 주장에 대하여 반대하였다.


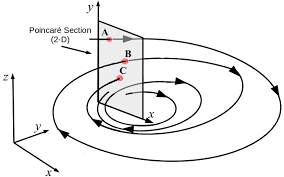
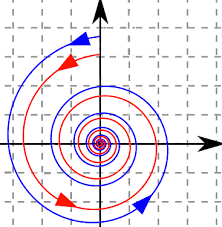
앙리 푸앵 카레는 “초기 변수의 민감성”을 통해서 아무리 정확하게 과학자들의 태양계의 최초상태의 성질이나 상태, 수학적 값들을 알더라도 과학자들이 모르는 변수가 하나쯤은 있을 것이며, 이 태양계의 최초 상태가 과학자들이 알던 값과 조금이라도 다르면 엄청난 오류로 이어지기 때문에 과학자들은 태양계의 미래를 예측하지 못할 것이라고 반박한다.
앙리 푸앵카레가 처음으로 제시한 “초기 변수의 민감성”에 대한 개념은 후에 혼돈 이론의 기초를 닦는 데에도 사용이 된다.

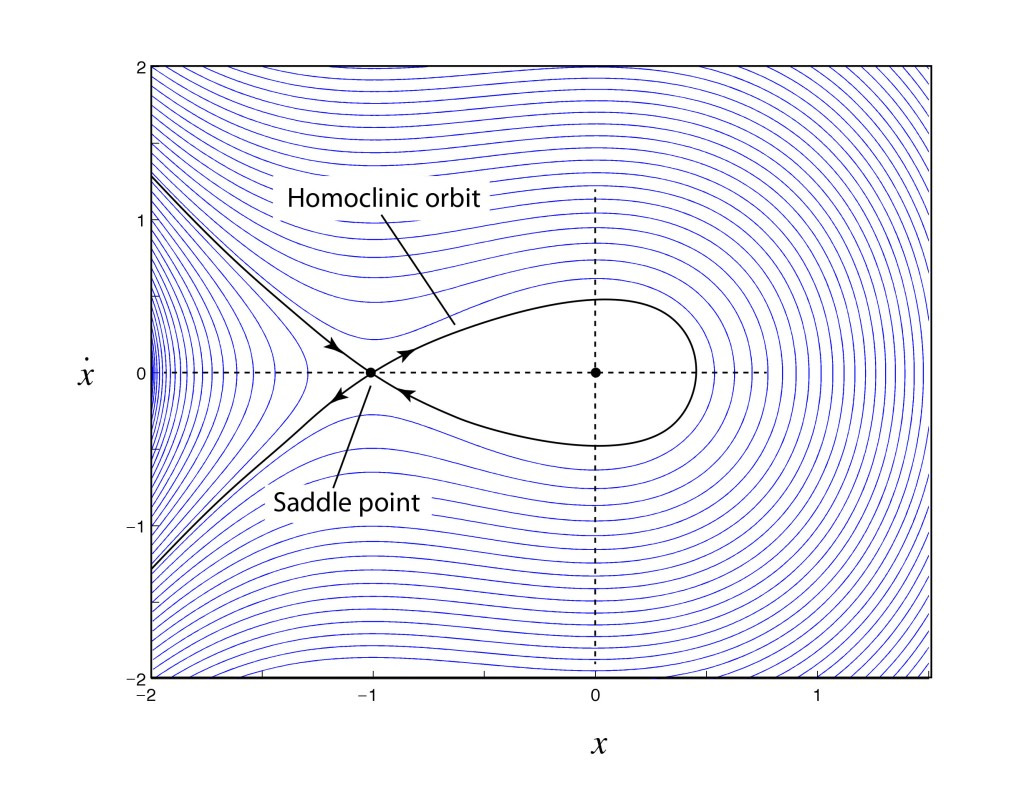


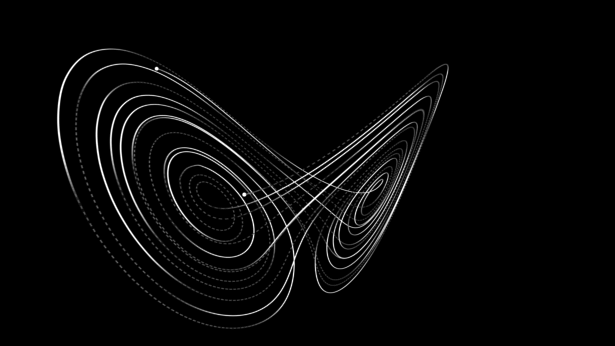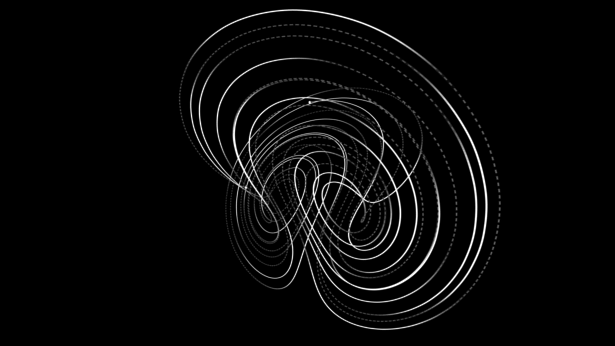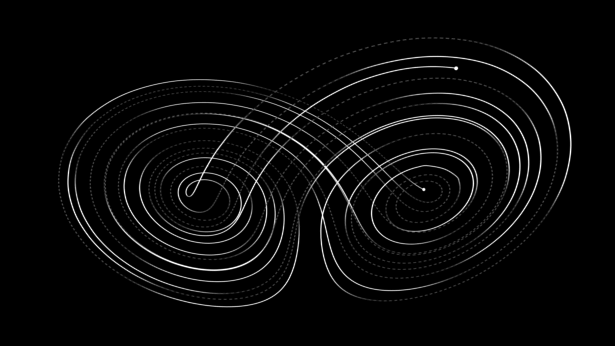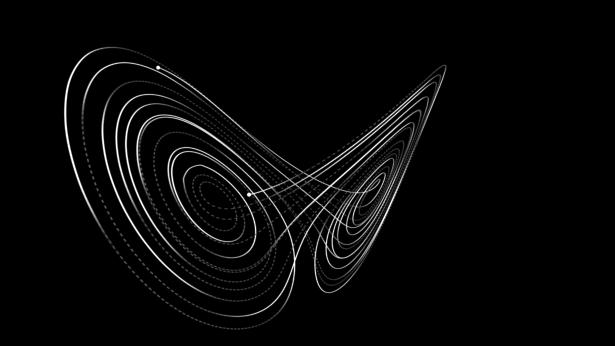
혼돈 이론의 탄생 – 에드워드 로렌츠(Edward Lorenz)
에드워드 노튼 로렌츠(Edward Norton Lorenze)는 메사츄세스 공과대학교(Massachusetts Institute of Technology (MIT))에 근무하던 기상학자이자 수학자로 자신이 똑같은 기상 관측 모델을 사용하여 날씨를 예측하였음에도 불구하고, 소수 세번째 자리까지 입력한 값과 소수 여섯번째 자리까지 입력한 값의 기상 관측 모델 결과 값이 완전히 다른 날씨 예측 결과가 나타나는 현상을 발견한다.



에드워드 로렌츠는 이 기괴한 현상을 비선형 계(시스템)에서의 혼돈(무질서함)이라고 한 학회에서 발표를 하였다.
하지만 이 학회를 주최하던 측에서는 이 에드워드 로렌츠의 발표 제목을 다음과 같이 제목 지으면서, 에드워드 로렌츠의 혼돈 이론은 나비 효과라는 이름으로 대중들에게도 알려지게 된다 “예측성 : 브라질의 나비의 날개짓이 텍사스의 토네이도로 이어질 수 있는가?“ 훗날 에드워드 로렌츠는 혼돈 이론을 제시하게 된다.
“Predictability: does the flap of a butterfly's wing in Brazil set off a tornado in Texas?”
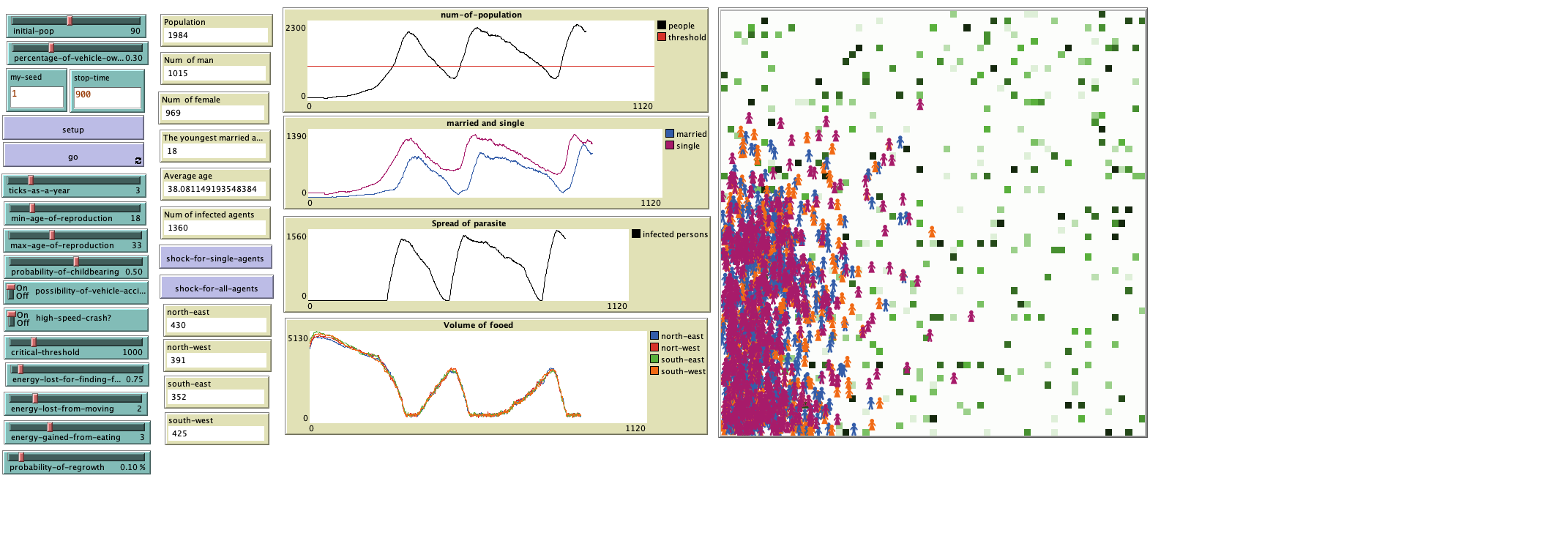
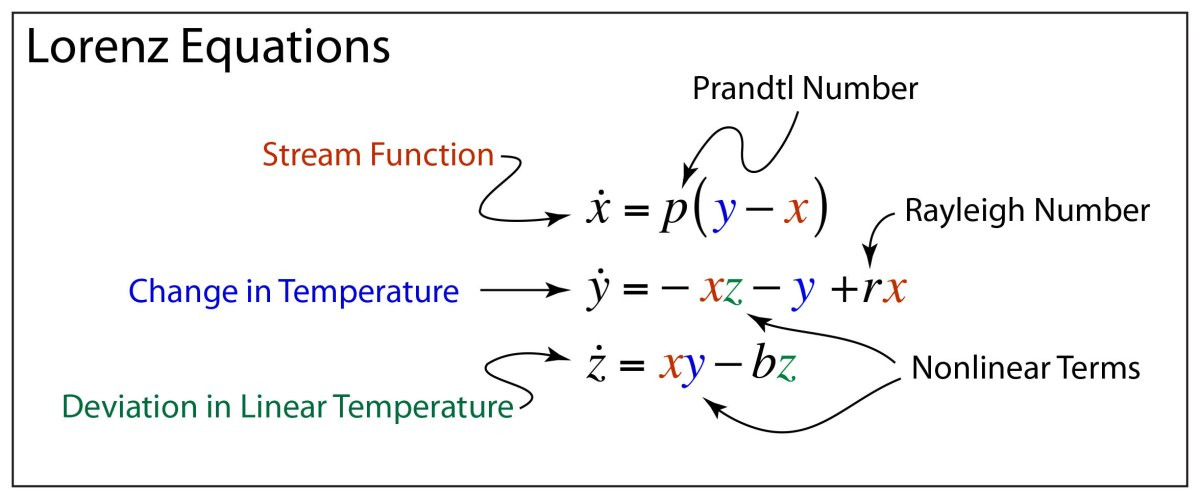
로지스틱 맵/로지스틱 사상 Logistic map – 혼돈이론으로부터 파생 된 수열
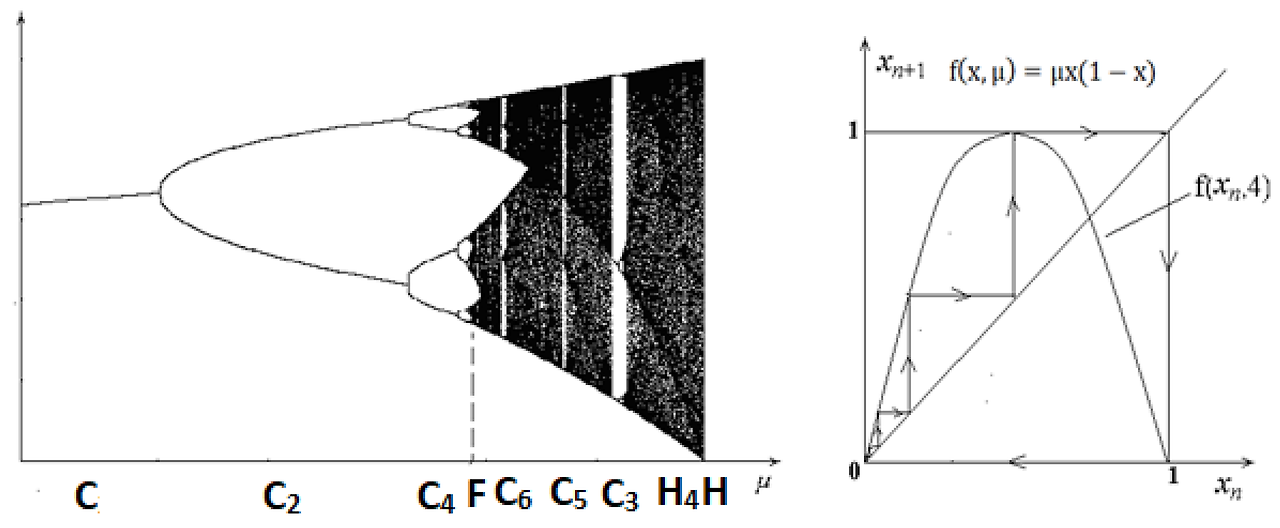
로지스틱 사상 또는 로지스틱 수열(Logistic Map)은 로버트 M. 메이(Robert M. May)라는 생물학자가 발견한 수열로 혼돈이론으로부터 파생되었다. 이 로지스틱 맵/수열은 아주 단순한 2차 함수이지만 혼돈/무질서한 성질을 띠는데, 이는 변수의 범위에 따라 함수의 값이 엄청나게 크게 변함을 의미한다.
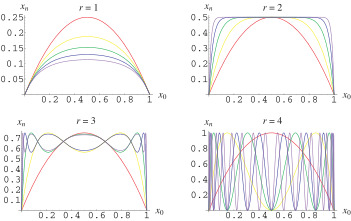
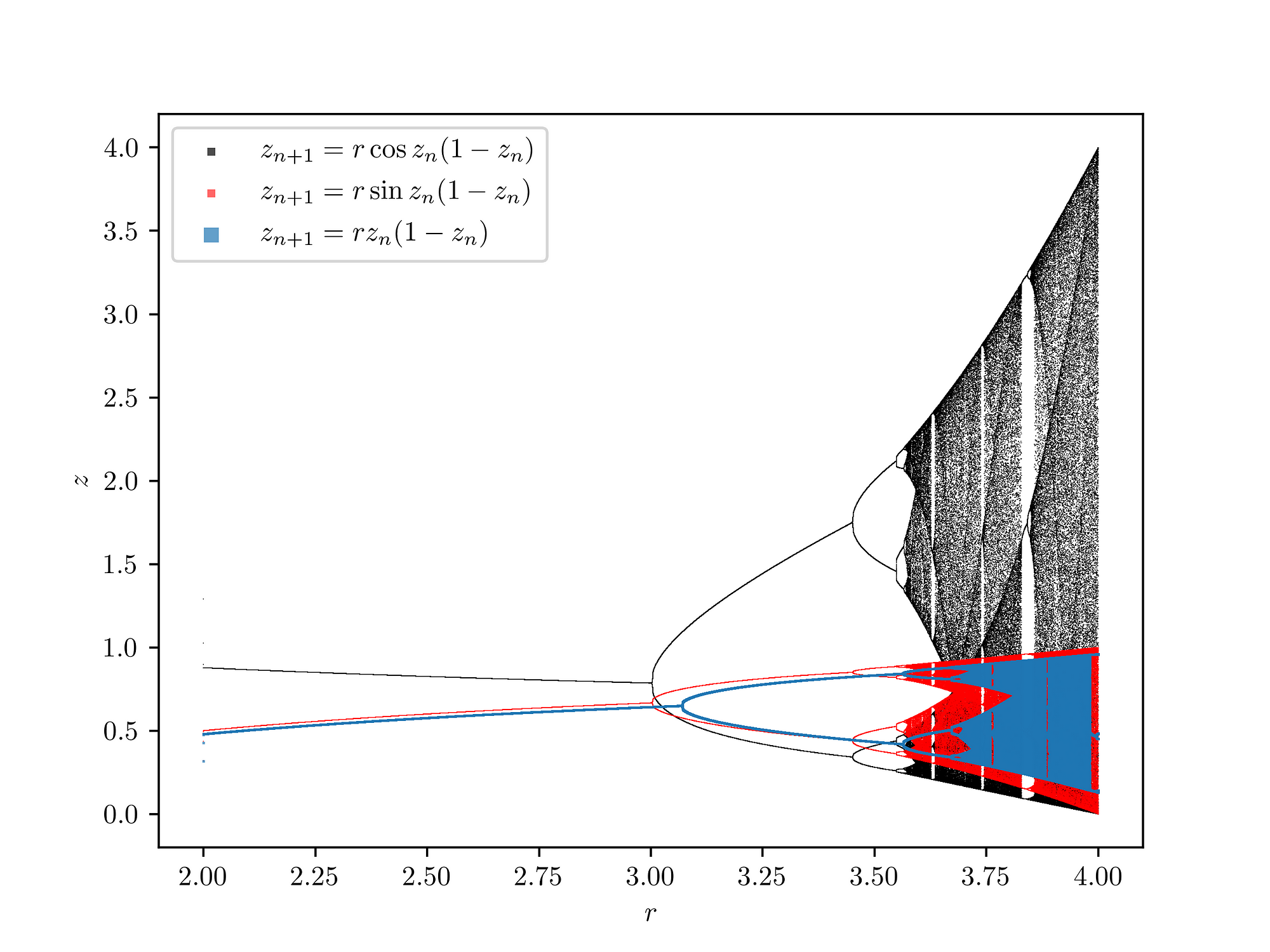
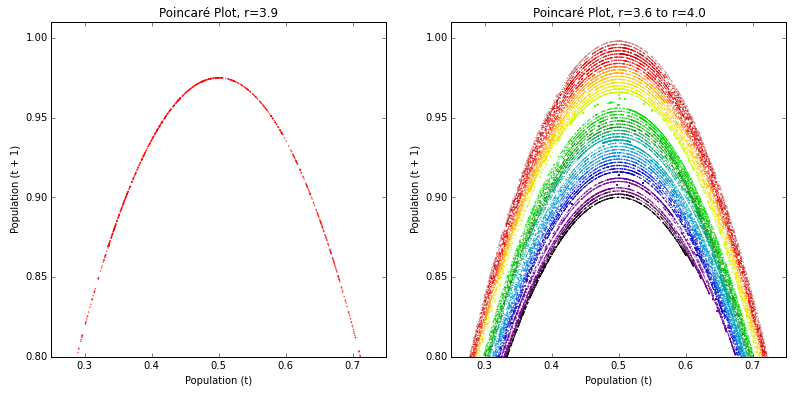
xn 은 0부터 1까지의 확률을 뜻하는 변수이며, r 변수의 범위에 따라서 이 로지스틱 수열의 값은 크게 혼돈 경향 즉, 매우 큰 변동성을 가진다. 이 로지스틱 수열/사상은 초기 값에 매우 민감한 함수의 하나의 예시며, 아주 간단한 함수가 얼마나 큰 무질서함, 즉 혼돈 성을 띨 수 있는지 보여주는 예시이기도 하다.
xn+1=rxn(1-xn)